Required Videos
Here are the required notes for your convenience.
Supplemental Videos
Two graphs may look exactly alike in shape, but differ in their positions within the xy-plane.
Adding or subtracting values from a function will shift the graph of the function on the coordinate plane.
If f is a function and c is a positive constant, then the graph of
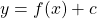 is the graph of
is the graph of 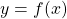 shifted up c units
shifted up c units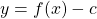 is the graph of
is the graph of 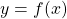 shifted down c units
shifted down c units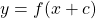 is the graph of
is the graph of 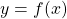 shifted left c units
shifted left c units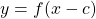 is the graph of
is the graph of 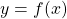 shifted right c units
shifted right c units
Vertical translations: adding or subtracting after the function (outside the parenthesis)
![]() shifts
shifts ![]() up 3 spaces on the y axis
up 3 spaces on the y axis
![]() shifts
shifts ![]() down 2 spaces on the y axis
down 2 spaces on the y axis
Horizontal translations: adding or subtracting with the function (inside the parenthesis)
![]() shifts the graph of
shifts the graph of ![]() left 4 spaces on the x axis
left 4 spaces on the x axis
![]() shifts the graph of
shifts the graph of ![]() right 3 spaces on the x axis
right 3 spaces on the x axis
Vertical & Horizontal translation
![]() shifts the graph of
shifts the graph of ![]() up 2 spaces on the y-axis and right 5 on the x-axis.
up 2 spaces on the y-axis and right 5 on the x-axis.
If ![]() ,
, ![]() , and
, and ![]()
Find the coordinates for h(x) = f(x) + 5 and g(x) = f(x – 2)
| | |||
| | |||